Finite blocklength information theory: Two recent results
Professor Yury Polyanskiy
Assistant Professor, MIT
Given on: April 9th, 2015
Venue: Packard 101
Time: 4:15pm to 5:15pm
Abstract
Finite blocklength information theory attempts to elucidate the fundamental performance-delay tradeoffs. Initial results (which I will overview) showed fluctuations of rate around the Shannon capacity to be Gaussian with variance inversely proportional to square root of the blocklength. Many subsequent results refined and strengthened this central-limit theorem (CLT) type analysis.
More recently it was discovered that some quite natural channel coding and data compression problems exhibit non-CLT type behavior. This talk will focus on two such results. Both effects arise due to the presence of multiplicative component in the channel noise. Besides theoretical interest, these results are practically insightful for the wireless communication systems as follows:
Analysis based on outage-capacity imposes contradicting assumptions: the blocklength should be small enough for the channel state to be almost constant, and it should be large enough for Shannon coding theorem to be effective. Practically, however, this method ‘‘just works’’. The first result explains why.
A classical result of Kennedy shows that the optimal energy efficiency (-1.59 dB per bit) is achievable even under multiplicative noise. Practically, this may suggest that the channel-state information (CSI) is useless for improving energy efficiency. Our second result shows this to be only true when communicating with huge packets of order
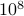 bits.
bits.
Biography
Yury Polyanskiy is an Assistant Professor of Electrical Engineering and Computer Science and a member of LIDS at MIT. Yury received the M.S. degree in applied mathematics and physics from the Moscow Institute of Physics and Technology, Moscow, Russia in 2005 and the Ph.D. degree in electrical engineering from Princeton University, Princeton, NJ in 2010. In 2000-2005 he lead the development of the embedded software in the Department of Surface Oilfield Equipment, Borets Company LLC (Moscow). Currently, his research focuses on basic questions in information theory, error-correcting codes, wireless communication and fault-tolerant and defect-tolerant circuits. Dr. Polyanskiy won the 2013 NSF CAREER award and 2011 IEEE Information Theory Society Paper Award. In 2012 Yury was selected to hold a Robert J. Shillman (1974) Career Development Professorship of EECS.